EUCLIDEAN DISTANCE–

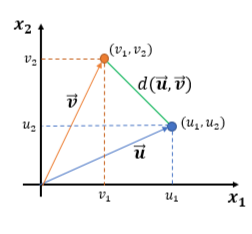
• Consider the points in two-dimension. Each point in two-dimension can be represented by a vector of dimension two.

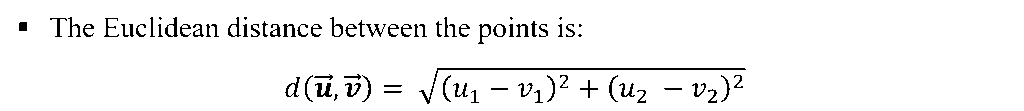
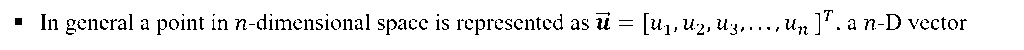
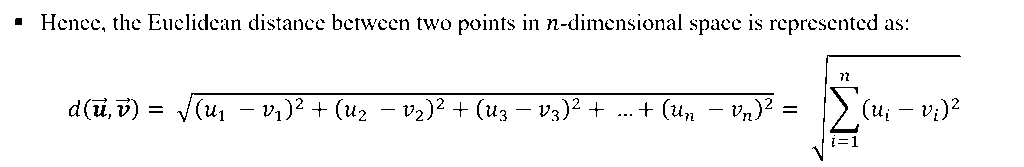
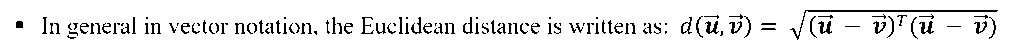
OTHER DISTANCE METRICS

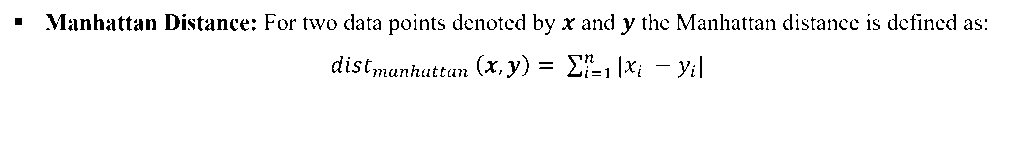
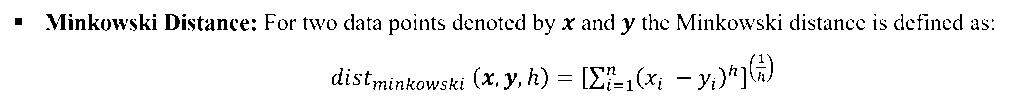
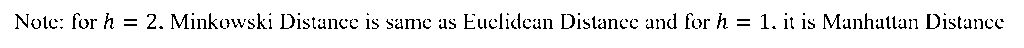
There are other distance metric like: Mahala Nobis Distance, Bhattacharya Distance etc. These are used for advanced statistical pattern recognition tasks.

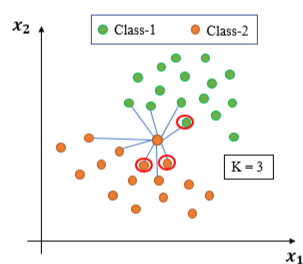
• K-NN Algorithm:

1. All the training samples/ points are available beforehand.
2. When a new test sample arrives calculate its distance from all training points.
3. Choose K-nearest neighbors based on the distance calculated. Usually, the K is a positive odd integer and supplied by user. 
4. Assign the class label of the test sample based on majority. i.e. for a test sample if most number of neighbors among those K-Nearest Neighbors belong to one particular class-c, then assign the class label of test sample as c.

• Characteristics of K-NN Classifier:

It doesn’t create model based on the training patterns in advance. Rather, when a test instance comes for testing, runs the algorithm to get the class prediction of that particular testing instance. Hence, there is no learning in advance.

-Hence, k-NN classifier is also known as Lazy Learner.

K-NN Classifier: Decision Boundary–

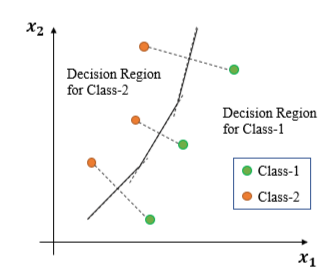
• Boundary are the points those are equidistant between the points of Class-1 and Class-2
• Construct lines between closest pairs of points in different classes.
• Draw perpendicular bisectors. End bisectors at intersections.
• Note that locally the boundary is linear.
• Hence the decision boundary is piece-wise linear curve.

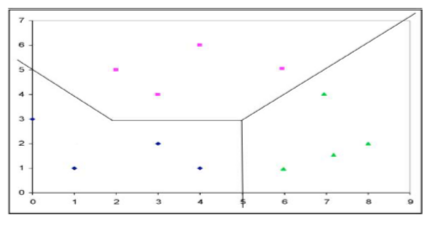
For multi-class classification also the same thing is done to find the decision boundary.

K-NN: Choosing the value of K–

Increasing the ‘K’ simplifies the decision boundary. Because majority voting implies less emphasis on individual points.

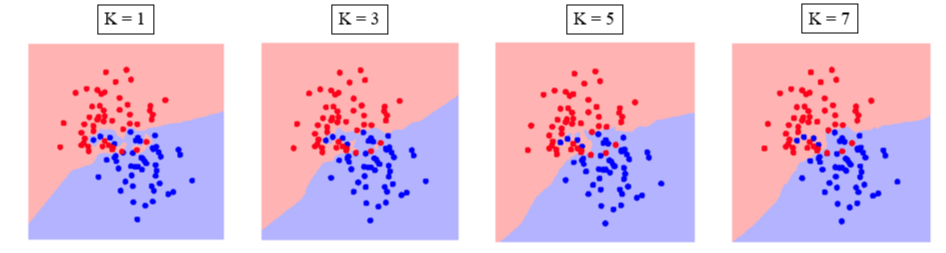
• However increasing the K also increases computational cost.
• Hence, choosing K is an optimization between how much simplified decision boundary we want vs. how much computational cost we can afford.
• Usually K = 5, 7, 9, 11 works fine for most practical problems.

Merits:

• K-NN Classifier often works very well for practical problems.
• It is very easy to implement, as there is no complex learning algorithm involved.
• Robust to Noisy Data.

Demerits:

• Choosing the value of K may not be straightforward. Often the same training samples are used for different values of K. But we choose the most suitable value of K based on minimum misclassification errors on test samples.
• Doesn’t work well for categorical attributes.
• Can encounter problem with sparse training data. (i.e. data points are located far away from each other)
• Can encounter problems in very high-dimensional spaces.
  •                   Most points are at corners.
  •                   Most points are at the edge of the space.

-This problem is known as Curse of Dimensionality and affect many other Machine Learning algorithms.